Specification languages: Programming languages, Extended state machine models and Petri nets

In the above chapters we have discussed basic state machine models which lead to global states with a finite number of states, except when input queues are unbounded. However, their simplicity is often not powerful enough to model all aspects of the system to be described. There are two solutions to this problem:

• Limit yourself to a simplified model of the system - using a basic state machine model, or
• Use a more powerful modeling paradigm which allows for additional state variables and interaction parameters of arbitary data types. In this case, there are again two possibilities:
  • Use a programming language for modeling the behavior.
  • Use a so-called extended state machine model which allows for additional state variables and interaction parameters. Each transition in an extended state machine has the following:
    • An enabling condition which depends on the local variables and the parameter values of the input received (if there is one). The transition can only be executed if this condition is true.
    • An update operation which defines new values for the local variables and values for the parameters of the output produced (if there is any). This update operation is performed when the transition is executed.

An extended state machine model and a programing model have many similarities:

• The states of the state machine model correspond to the different points in the control flow graph of the program where the current point of execution may reside.
• Both have (additional) state variables.
• Input and output of messages with parameters, like in extended state machine models, can be modeled in a program by predefined methods send and receive.

However, behavior specifications for communication protocols and system requriements, in general, are often nondeterministic (in a given state, different outputs may be produced, or the values of certain output messages may be underfined). On the contrary, normal programming languages are normally deterministic. Also, programming languages are often quite complex, and the defined behavior may not be clear to the reader.

For these reasons, Dijkstra proposed in 1975 the Guarded Command Language (see Wikipedia) which is very simple and helps the understanding (and possibly proving) of properties of a given program. This language was later adapted by Holzmann in the Promela language which is used with Spin.

Petri nets also represent a generalization of the basic state machine models of LTS and IOA. A single Petri net may model several concurrent activities (there may be several tokens simultaneously within the given Petri net), as well as data flow between them or mutual exclusion for shared resources. Message passing can be modeled by a token which goes from one place of the Petri net to another place - each place holds only messages of a given type. - In order to model messages with parameters, Petri nets have also be extended, and are called Colored Petri Nets, Predicate Transition Nets, or similar. These extensions are as follows:

• A token may have several parameters (of specific data types) which take on specific values. Therefore a token may represent a message with its parameter values, but it may also represent the instance of a process (that is, state machine) where the token parameters represent the local variables of that process (or state machine). Each place has a type which defines the type of tokens that may reside there.
• Each transition of the Petri net is associated with an enabling predicate and an update operation. The enabling predicate depends on the parameters of the tokens that are required for the transition. And the update operation defines the parameter values of the tokens that are produced by the transition. (Note: this is very similar to the enabling condition of the extended state machine model and the update operation of state machines that define new values of the local variables and the values of output parameters).

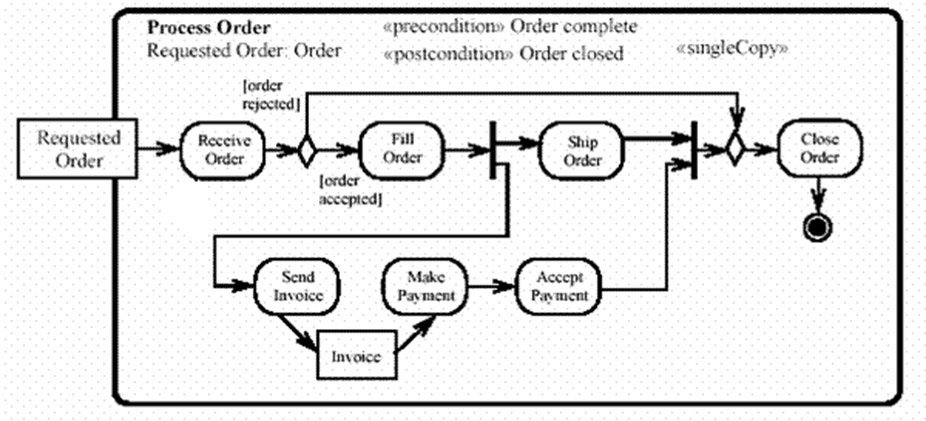
We note that the formalism of extended Petri nets has been used to define the semantics of UML Activity Diagrams. The explanation of their semantics talks about tokens that go from one activity to the next. These tokens may represent data flow, in which case one would consider extended Petri-net tokens with parameters. See example below.

Created: October 2014